Direct Transcription of Low-Thrust Trajectories with Finite Trajectory Elements
Apr 1, 2012·, ,·
0 min read
,·
0 min read
Federico Zuiani
Massimiliano Vasile
Alessandro Palmas
Giulio Avanzini
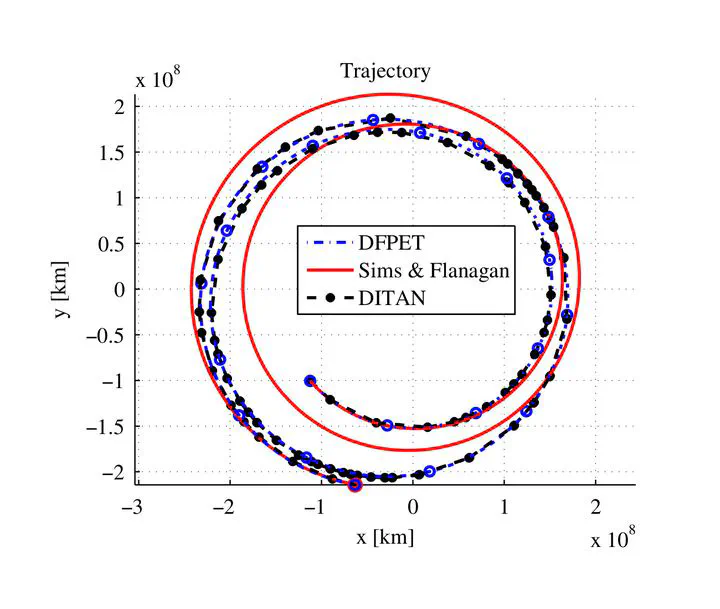 Optimized trajectories comparison
Optimized trajectories comparisonAbstract
This paper presents a novel approach to the design of Low-Thrust trajectories, based on a first order approximated analytical solution of Gauss planetary equations. This analytical solution is shown to have a better accuracy than a second-order explicit numerical integrator and at a lower computational cost. Hence, it can be employed for the fast propagation of perturbed Keplerian motion when moderate accuracy is required. The analytical solution was integrated in a direct transcription method based on a decomposition of the trajectory into direct finite perturbative elements (DFPET). DFPET were applied to the solution of two-point boundary transfer problems. Furthermore the paper presents an example of the use of DFPET for the solution of a multiobjective trajectory optimization problem in which both the total ∆V and transfer time are minimized with respect to departure and arrival dates. Two transfer problems were used as test cases: a direct transfer from Earth to Mars and a spiral from a low Earth orbit to the International Space Station.
Type
Publication
Acta Astronautica, Volume 72, March–April 2012, Pages 108-120